AES, also known as the Advanced Encryption Standard, is one of the fundamental building blocks of today’s secure communications. It is inside almost everything connected. If it is not in there, it probably should be!
We rarely ask ourselves the question, what’s inside it? As it turns out, most of the time we are comfortable not knowing and trusting this little black-box. Its content isn’t exactly comparable with a fancy new framework. It is a healthy mixture of math and some low level bit manipulation.
However, there is beauty inside this beast. It is as elegant as it gets, and it is very powerful. Once you understand it, you can explain it to a 5-year-old. This is the aim of this post, to help you explore the little world inside one of the most common black-boxes of security. Let’s go!
Our approach
Learning and discovery is our human nature. We look at complex problems and deconstruct them. We use familiar tools to analyze and understand more and more of the little pieces. In time, we can put the parts back together and comprehend the system as a whole. This is what we’ll do here. We’ll take AES apart, look at the pieces using tools we’ve mastered (code and tests). And then, assemble it back together.
By the end of the post, you’ll completely understand and even appreciate the simplicity and elegance of AES. During our journey, you’ll also learn a few crypto concepts.
The pieces to the puzzle
Before we jump into the nitty-gritty details, there is a term you should be familiar with: diffusion. It’s from an essay titled “A Mathematical Theory of Cryptography” by Claude Shannon. Feel free to read the paper on your sleepless nights.
Here is what it says about diffusion.
In the method of diffusion the statistical structure of M which leads to its redundancy is “dissipated” into long range statistics — i.e., into statistical structure involving long combinations of letters in the cryptogram.
Sounds cool? Maybe, for some!
To the rest of us, diffusion refers to the relation between the plaintext and ciphertext. It states that a change of a single bit in the plaintext should cause roughly half of the ciphertext bits to change, statistically of course. In other words, diffusion is required to destroy the patterns in the plaintext input.
It is commonly achieved by repetitive use of permutations and substitutions. This is precisely what AES does.
The concept of a round
AES is built up of rounds. For our purposes, we’ll look at the encryption process of AES-128-ECB (simplest mode with a 128-bit key). This mode has 10 rounds.
A round consists of the following operations in order: SubBytes, ShiftRows, MixColumns, AddRoundKey. The terms are from the original whitepaper for easy reference.
AES is a block encryption. It works on chunks of data at a time. The block size of AES is 128 bits or 16 bytes. The operations described below operate on 4x4 matrices.
SubBytes
This is as simple as it gets. All it does is looks up values from a 16x16 table defined by the whitepaper. This table is also referred to as an S-box or substitution box. Now, this is not just any table, it is designed to destroy patterns!
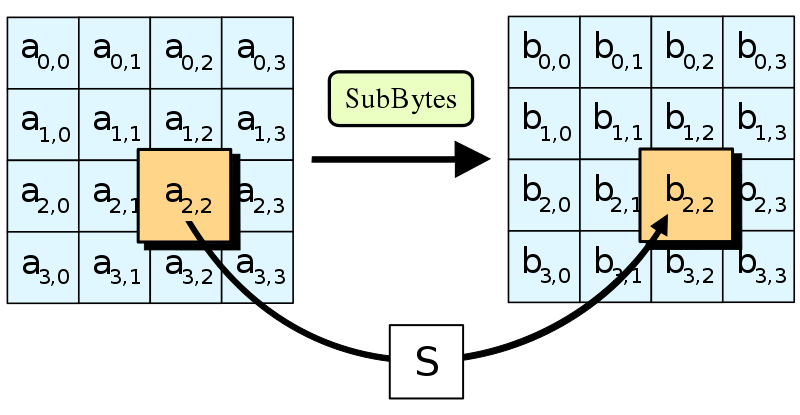
Here is the relevant code snippet from the repository.
class ByteSubstitutor {
constructor(sBox) {
this._sBox = sBox;
}
get(byte) {
return this._sBox[Math.floor(byte / 0x10)][byte % 0x10];
}
}Not much to talk about, it’s an array indexing operation.
ShiftRows
Increasing complexity! The next operation moves bytes around in an array. Again, the aim is to destroy any existing patterns.
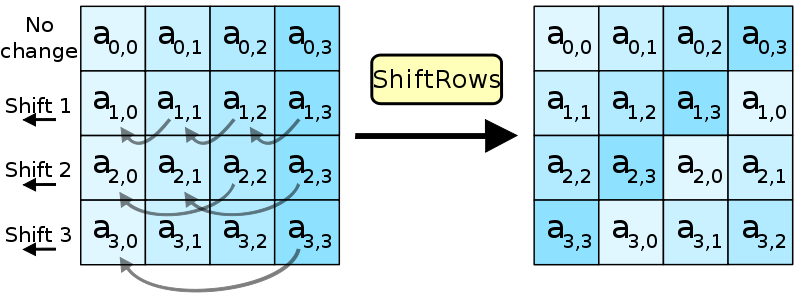
Here is the relevant code, nothing too complex.
class WordRotator {
static rotate(word, count) {
if (count === 0) {
return word;
}
const rotated = [
word[1],
word[2],
word[3],
word[0]
];
return WordRotator.rotate(rotated, count - 1);
}
}
class RowShifter {
static shift(block) {
return block.map(
(word, i) => WordRotator.rotate(word, i)
);
}
}Where is all the crypto stuff?
MixColumns
This step is a bit more complicated, but nothing you can’t handle. Now we are working on columns, and apply a c(x) transformation to each.
For the little math lover within you, here is the excerpt from the whitepaper:
[..] treating each column as a four-term polynomial [..]. The columns are considered as polynomials over GF(2) and multiplied modulo x⁴ + 1 with a fixed polynomial a(x), given by a(x)={03}x³+{01}x²+{01}x+{02}.
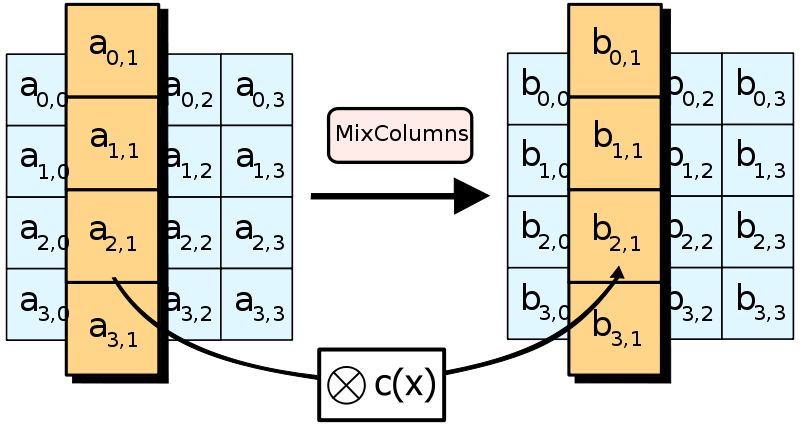
As it turns out, this is scarier on paper than in code. Check it out!
class ColumnMixer {
static mixBlock(block) {
return Util.transpose(
Util.transpose(block).map(
word => ColumnMixer._mix(word)
)
);
}
static _mix(word) {
return [
m2(word[0]) ^ m3(word[1]) ^ word[2] ^ word[3],
word[0] ^ m2(word[1]) ^ m3(word[2]) ^ word[3],
word[0] ^ word[1] ^ m2(word[2]) ^ m3(word[3]),
m3(word[0]) ^ word[1] ^ word[2] ^ m2(word[3])
];
}
}Util.transpose(…) inverts the columns and rows of the matrix, as we are operating on columns now. Here, we transpose the block, apply the mixing and transpose it back.
m2(…) and m3(…) are substitutions just like SubBytes above but with a different table. Under the surface the S-boxes used here are multiplication tables (of 0x02 and 0x03 over GF(8)).
^ is a binary XOR.
That’s about it. Should you feel the need to dive in more deeply, read section 5.1.3 from the AES whitepaper and explore Galois Fields. Onward!
Add(Round)Key
At the heart of every encryption scheme is the key used to encrypt the data. Up till this point, we haven’t done anything with the key yet. This is where the “real encryption happens” and, just like in the movies, it is a “very sophisticated” XOR (⊕) operation.
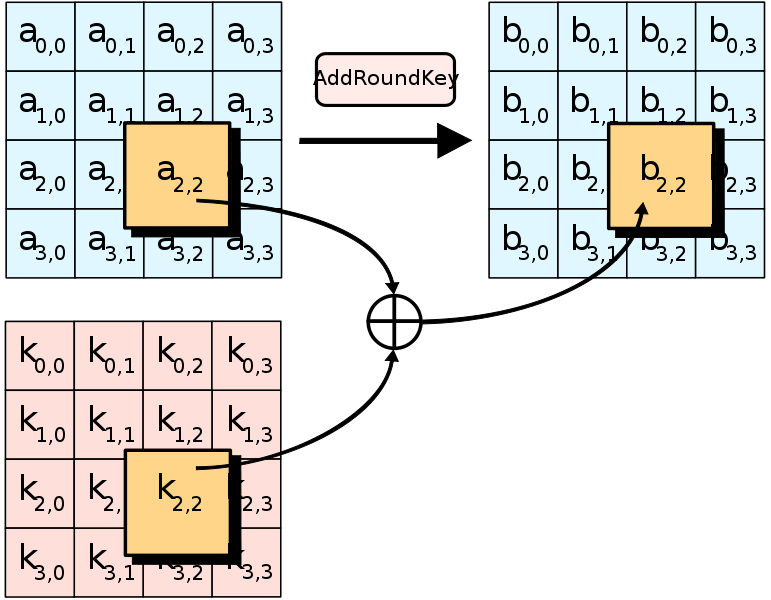
Here is the code. If only there was a zip function in Javascript…
class Util {
static xorBlock(blockA, blockB) {
return [
Util.xorWord(blockA[0], blockB[0]),
Util.xorWord(blockA[1], blockB[1]),
Util.xorWord(blockA[2], blockB[2]),
Util.xorWord(blockA[3], blockB[3])
];
}
static xorWord(wordA, wordB) {
return [
wordA[0] ^ wordB[0],
wordA[1] ^ wordB[1],
wordA[2] ^ wordB[2],
wordA[3] ^ wordB[3]
];
}
}Now, that the key is in the process, we are all good. Encryption complete!
Well, not exactly. The Key is not the RoundKey.
Yep, for each round of AES, there is a different key. To calculate such a RoundKey we’ll use a concept called key expansion.
Key expansion
This is essentially the generation of keying material from the initial key we received during input. This is probably the most complex part of the whole scheme. Before we get into it, let’s get familiar with a concept called confusion.
Confusion refers to the relation between the key and the ciphertext. From Wikipedia:
[..] each binary digit (bit) of the ciphertext should depend on several parts of the key, obscuring the connections between the two. […]
In other words, the result of the encryption should be highly dependent upon the key. Makes sense, right?
This is achieved by repeatedly shuffling (see above) the plaintext and applying a round key. It is calculated by the following code:
01 class KeyExpander {
02 getRoundKey(round) {
03 if (round === 0) {
04 return this._key;
05 }
06 const previousRound = Util.transpose(
07 this.getRoundKey(round - 1));
08 const state = Util.xorWord(
09 SubWord(RotWord(previousRound[3], 1)),
10 ROUND_CONSTANT[round - 1]
11 );
12 return Util.transpose(
13 this._calculateRoundKey(state, previousRound));
14 }
15 _calculateRoundKey(state, previousRound) {
16 let roundKey = [];
17 for (let i = 0; i < 4; i++) {
18 state = Util.xorWord(state, previousRound[i]);
19 roundKey[i] = state;
20 }
21 return roundKey;
22 }
23 }This may look cryptic at first. Let’s decipher, no pun intended :)
Without looking too hard, we see a recursion (line 07). So, the current round’s key depends on the previous round’s key. Makes sense! (This is called the avalanche effect, a simple change in the input causes a significant change in the output.)
Then, there is some shuffling bits around with known transformations (line 09). And adding a so-called round constant to the mix (line 10).
Finally, there is some “magic” in the _calculateRoundKey() (line 15) method. It takes the previous round’s key and XORs it with the current state.
See 5.2 Key Expansion in the AES whitepaper for more. Here is an excerpt to get you in the mood.

All good! Now that we have every part, let’s assemble the beast and test it!
Putting it all together
First, a quick visualization of how the whole thing should look. We are discussing the process on the left.
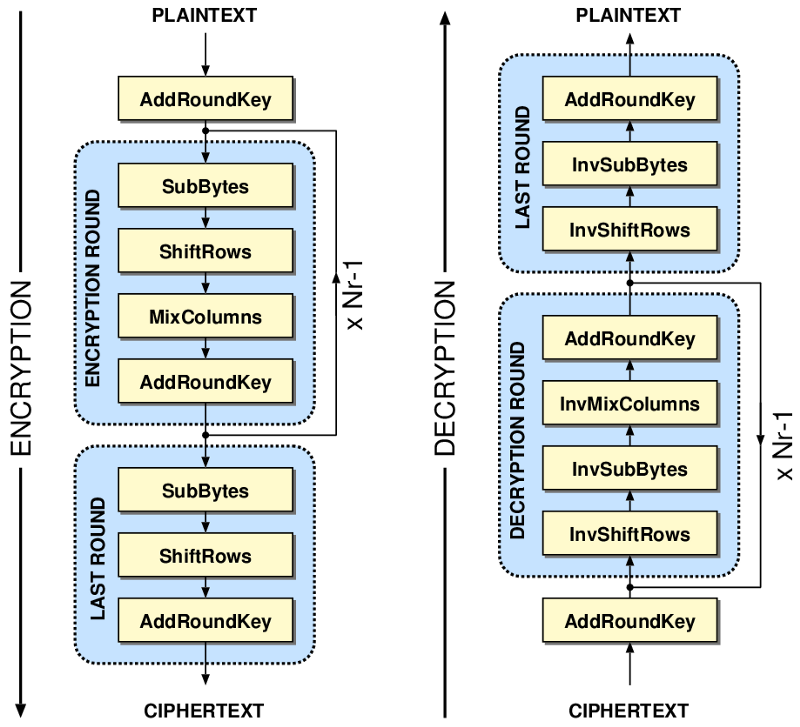
Enough said, show me the code!
class Encryptor {
static encrypt(key, plaintext) {
let stateBlock = Util.bufferToBlock(plaintext);
const keyBlock = Util.bufferToBlock(key);
const keyExpander = new KeyExpander(keyBlock);
stateBlock = Util.xorBlock(
stateBlock, keyExpander.getRoundKey(0));
for (let i = 1; i < 10; i++) {
stateBlock = SubBytes(stateBlock);
stateBlock = ShiftRows(stateBlock);
stateBlock = MixColumns(stateBlock);
let roundKey = keyExpander.getRoundKey(i);
stateBlock = Util.xorBlock(stateBlock, roundKey);
}
stateBlock = SubBytes(stateBlock);
stateBlock = ShiftRows(stateBlock);
let roundKey = keyExpander.getRoundKey(10);
stateBlock = Util.xorBlock(stateBlock, roundKey);
return Util.blockToBuffer(stateBlock);
}
}Nothing should surprise you, you know all the details.
So, does it work?
it('encrypts like built-in AES', () => {
const key = Buffer.from([...]);
const plaintext = Buffer.from([...]);
const cipher = crypto.createCipheriv('aes-128-ecb', key, null);
const aesOutput = cipher.update(plaintext);
cipher.final();
expect(Encryptor.encrypt(key, plaintext)).to.eql(aesOutput);
});Well, of course! Try it for yourself by running npm t in the repo.
Encryptor
#encrypt
✓ encrypts like built-in AES
1 passing (8ms)Takeaways
AES is a simple, yet very elegant beast. You have a good understanding of how it works. The next step is to go and explain it to someone else. During our journey you also encountered a few important crypto concepts: diffusion, confusion, key-expansion, and the avalanche effect. All by doing stuff you already know, reading code and reasoning.
All the code is in a repository. Feel free to play around with it. Obviously, it is for educational purposes only, and not meant to be used anywhere. If you want to dig deeper, check out the AES whitepaper, and the original Rijndael proposal.
Now go!
Blackboxes look immensely complex until you take a peek inside. Taking the time to understand them will grow your knowledge and arm you with a can-do mindset. Use tools you already know and understand. Who knows, you may pick up a few techniques and tools in the process. Learn and discover, it’s in your nature!
Thanks for joining the journey! Now go and find a black box to take apart!
This post originally appeared on the Craftlab blog.
